Modified IRR – MIRR (Modified InternalRate of Return)
Like IRR, MIRR characterizes the discount rate at which the total present value of income is equal to the value of investments. The calculation of the modified value of IRR, for a full understanding, it can be expanded in steps:
step 1. All values of income (positive amounts, in the tributaries, CF+n) are given by the end of the project. For conversion, the rate equal to the weighted average cost of capital is used:
(1+WACC)+(N - n).
2 step. All investments and reinvestments (negative amounts – outflows, CF-n) are given to the beginning of the project. To bring the discount rate used:
(1 + r)-(n - 1).
Reinvestments in fact – aimed at the development of cash (current and non-current assets).
step 3. MIRR is defined as the rate of return at which all expected revenues given by the end of the project have a present value equal to the cost of all required costs:
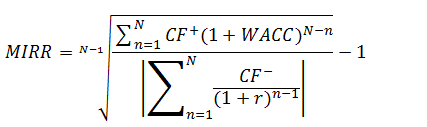
CF+n – incomes of the n-th period (positive values)
CF-n – costs, (investments, reinvestment) of the n-th period
WACC – weighted average cost of capital
r – discount rate
N – duration of the project
The calculation MIRRis relevant for cases where cash flows are non-standard, that is, there are both positive and negative flows during the project implementation. The project is acceptable to the initiator, if MIRR is more effective barrier rate.
Also, as in the calculation of other indicators, the formula uses the discounting step specified by the user.
Budget-Plan Express is a software product for preparing business plans and presentations in Word and Excel format - for small businesses and studies (students, MBI students, etc.)
Calculate project performance indicators (РВ, DPB, NPV, PI, IRR and others) in the new version of the program (6.02) More ...
Explanations to the MIRR formula and recommendations for calculations
☛ Note that only net cash flow is used to calculate the internal rate of return of IRRs and the modified internal rate of return for MIRR. Also, the result of calculations is influenced by the discounting step chosen by the user.
The meaning of the formula comes from the assumption of equality of discounted amounts of project financing, as well as reinvested funds (in this case, "outflows" in the net cash flow) and revenues - positive amounts (in this case, "inflows" in net cash flow).
![MIRR (MIRR factor) that needs to be found from the formula [1]. That is, the MIRR formula [2] is nothing more than an equivalent conversion of equality [1]](img.files/help-168-derive-formula-MIRR.gif "How to derive the MIRR formula (Modified Internal Rate of Return)")
|
[1] |
Please note that for the discounting of positive amounts, the MIRR rate (MIRR coefficient) is used, which must be found from the formula [1]. That is, the formula MIRR [2] is none other than an equivalent transformation of equality [1].
Formula MIRR (Modified Internal Rate of Return):
|
|
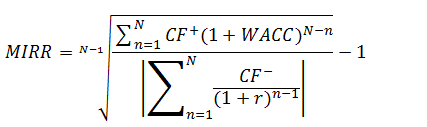
[2] |
-
Where:
CF+n – incomes of the n-th period (positive values),
CF-n – costs, (investments, reinvestment) of the n-th period,
WACC – weighted average cost of capital,
r – discount rate,
N – duration of the project
☛ Note that to calculate the modified internal rate of return of MIRR, a weighted average discount rate is used - for the entire calculation period selected by the user.
For an example of calculating MIRR, see «Features of the calculation of cash flows in Budget-Plan Express».
Select your Budget-Plan Express licenses and pay in your personal account - in rubles or other currency
