Features of the calculation of cash flows in Budget-Plan Express
Features of the calculation of cash flows in Budget-Plan Express
To calculate investment performance indicators (PB, DPB, NPV, PI, IRR and others), first of all, it is necessary to determine: what should be considered as initial investments and net proceeds? By and large, in practice two methods of determining initial investments and net receipts that can be selected in the program using settings are common (see section "General settings. Investment analysis"):
-
1 way . Initial investment is defined as a schedule of the need for working capital and other assets required for the project (net financing requirement).
2 way . Initial investments are all sources of financing - as the sum of capital costs and other costs for working capital, investment and other assets.
And in the first and second cases, you need to find a net cash flow, then - net investment and income. In both cases, the resulting indicators can not fundamentally differ from each other (or slightly differ), if in the second method the financial resources were optimally selected.
See also formulas for calculating integral indicators (PB, DPB, NPV, PI, IRR and others) in the section «Indicators of efficiency of investments. Calculation of key performance indicators in the Budget Plan Express».
Budget-Plan Express is a software product for preparing business plans in Word and Excel format. In the calculations of integral indicators (PB, DPB, NPV, PI, IRR), use any of the methods for determining the initial investment (calculation settings). Try the new version of the program (6.02).
This is the most affordable professional product in its class, and optimal for small businesses and studies (for students, MBI students, etc.) Details ...
Methods for determining initial investment
And in the first and second cases, you first need:
1 . Get net cash flow (NCF). To this end, financing (credit financing and equity instruments) is completely excluded from the total cash flow, and all financial payments, as a rule, to repay loans, are "returned".
2 . Then you need to find the net investment (net financing requirement) using the following algorithm:
-
❶ Net cash flow is considered a cumulative result.
❷ In this series (cumulative), the first negative amount of the series relates to investments.
❸ In subsequent negative amounts of the series, only negative growth is considered an investment, and after any positive amount, the increment accounting is interrupted - until the first negative amount appears, etc.
3 . Finally, when the net (absolute) need for funding is determined, one can find net proceeds. Net investment is deducted from net cash flow (NCF) for this purpose.
Further, depending on the chosen method, in the calculation of integrated indicators, net proceeds and initial investments will be compared, where the initial investment in the first case is a pure need for investments, in the second - the sources of financing used.
☛ Most often, in most programs, one method is used, which in turn is considered a "classical" way of determining initial investment. In Budget-Plan Express you can use any of the 2 ways (see section "General settings." Investment analysis).
How to find out the net need for financing after the development of operational plans, before the calculation of investment indicators?
☛ Note that the program will not allow the calculation of financial and investment indicators as long as there are negative values in the cash balance at the end of the period.
Before selecting the appropriate financing scheme, that is, immediately after the development of operational plans, look at the "end of period cash flow" graph (right-click). Below is the corresponding schedule (see construction project).
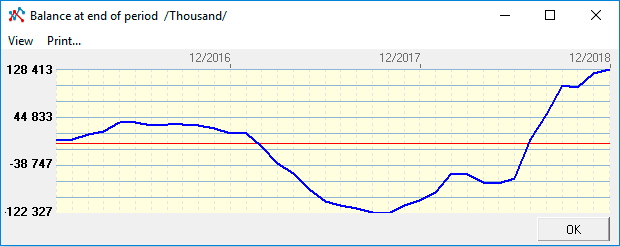
Note, after the development of all operational plans, before starting to attract any financial resources (credit, leasing or investment), always look at the chart of the Cash Flow line "balance at the end of the period ". To do this, after calculating all operational plans and part of the financial plans (except balance), you need to enter the Cash Flow line "balance at the end of the period" and call the chart (right mouse button), as shown in the figure.
Pay attention, the scale of the schedule - in thousands of rubles, means an absolute shortage of cash - 122 million 327 thousand rubles. Since the schedule goes to the negative zone once, this amount (122 million 327 thousand) is a net investment or a pure need for financing the entire project.
✎ Calculate the net funding requirement using the Budget-Plan Express software product. Try the new version of the program (6.02).
The result of the calculation in the first and second way can be the same or close if the project financing amounts are close to the real need for financing. For example, if the real need is 9,900 thousand (determined in the first way), and a loan of 10,000 thousand is issued, this means that the program will "seek" a payback point when returning 10,000 thousand (second way).
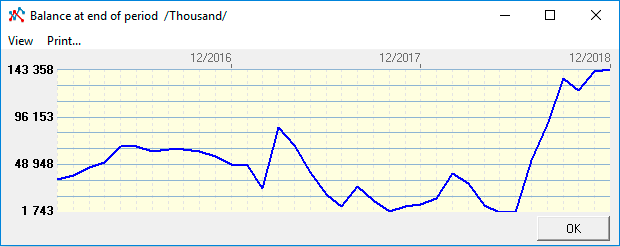
Thus, calculations in different ways can complement each other to identify suboptimal financing schemes. Below is an example of a graph of the same project (see construction project), where the financing scheme is selected sufficiently close to the real need.
The schedule of "cash balance at the end of the period" after financing, in thousands of rubles:
Algorithm of calculation in determining initial investments in different ways
When using the calculation algorithm in the first way, the flag "The need for financing (not discounted for the first year)" or "The need for financing (discounted)" is set.
If the flag "The need for financing (not discounted for the first year)" is set, it means that the financing needs will be calculated, where the first year the investment flow is not discounted, since it is assumed that the total investment is included in the project from the beginning its calculation (the calculation start period is determined by the user).
Accordingly, if the "Requirement for financing (discounted)" flag is set, this means that all amounts of the calculated funding requirement will be discounted in the period where the negative growth was registered (including 1 year of the project).
In either case, the following calculation algorithm is executed. At the first stage, all amounts associated with financing are excluded from the cash flow: proceeds from the issue of equity instruments, proceeds from loans and repayments of loans. If the exclude interest on loans is set, in this case, when calculating the funding requirement, the program will determine the net funding requirement or net investment (excluding interest). In other words, such an algorithm of calculation allows to determine the absolute need for investment resources - net investments (see tables 1 and 2). Then, a positive cash flow is determined.
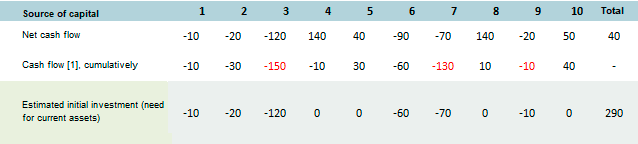
Example of calculating the need for current assets. Table 1 :

Find a net need for investment, within the limits of the cash deficit period, without resorting to calculations, for this it is sufficient to determine the minimum amount (the maximum need for financing) in a line reflecting the cash flow cumulative. In our case, this is the sum of "-150". However, if the negative cash flow is interrupted and then resumed again, all subsequent minimum amounts (the maximum need for financing) are added to the current amount.
The following table shows an example where there are three periods of cash deficits, and accordingly, the net demand for investments will be | -150 | + | -130 | + | -10 | = 290.
Example of calculating the need for current assets. Table 2 :
When using the calculation algorithm in the second way, the "Sources of financing" flag is set, that is, all sources of financing will be included in the initial investment directly in the period in which they were made. In this case also, at the first stage, all amounts related to financing are excluded from the cash flow: proceeds from the issue of equity instruments, proceeds from loans and repayments of loans. Then, all negative values are excluded from the cash flow, and thus a positive cash flow is determined.
Since the sources and periods of funding are determined, all amounts will be discounted in the period in which they were incurred. If the flag "Take into account future investments" is not set, the investments of the first year of the project will be taken into account, then the total cash flow will be taken into account. The remaining settings are identical for calculation in the first and second way.
Peculiarities of calculating the payback period
Sometimes there are situations when it is difficult to avoid incorrect calculations, and it is impossible to perform the calculation of integrated indicators within the calculation period of one project in the usual way. For example, when there are situations with multiple payback periods, respectively – several NPV, etc.
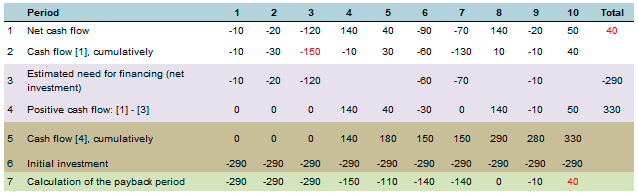
Example of payback period calculation. table 1:
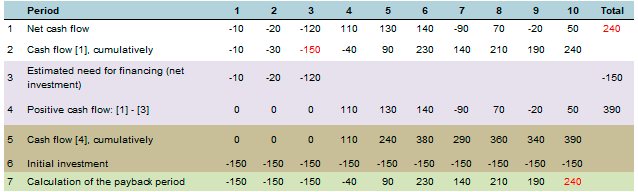
In the second table, the calculated funding requirement is also shown at the beginning of the period, however, after the fixed payback period in 8 months, in 9 months-again negative amount, that is, it turns out two payback periods, respectively two NPV, etc. How in this case, to determine the payback period and other indicators? Financial mathematics does not give an unambiguous answer to these questions. Provided that the last period on the payback period Calculation line is positive, the program adjusts the payback period calculation in this case as follows:
PB = N – N+ + 1,
Where:PB payback period;
N – total periods;
N+ – of all periods with a positive value.
Of course, in most cases you have to deal with the usual calculations, however, the value of the methodology inherent in the program is that it "finds" the right solutions for complex and non-standard calculations.
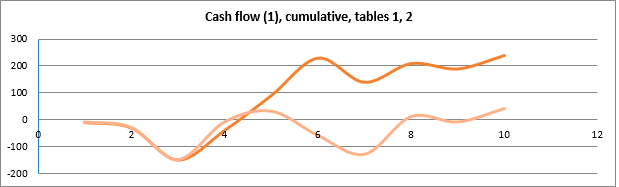
Example of payback period calculation. table 2:
☛ note the "cash flow (1) cumulative" graph for table 2 – the graph line three times "subsides" below the payback point, as opposed to the graph line of the same row in table 1, where the graph, after a temporary decline, grows in the "payback zone". In other words, if we consider "investments in the chart" without resorting to analysis, we can see the instability of the cash flow in the second case, and how in this case the trend of the chart affected the calculation of the payback period (see the line "calculation of the payback period").
For the sake of justice, it should be noted that in the vast majority of projects, such situations usually do not arise, since the maximum need for investment resources falls at the beginning of the calculation period. Even if the maximum need for investments falls on the middle of the project (as, for example, in construction projects), the period of negative cash flow still remains uninterrupted in most projects.
However, it must be remembered that the main value of integrated indicators, first of all, in determining the boundaries of investment and financial risks inherent in the project. For example, if a project is financed mainly from borrowed sources, it is necessary to include the interest paid to determine the risks based on the real need for financing.
☛ Notice the "influence of cash equivalents" is excluded from the cash flow by default.
Also, you can exclude interest on loans and dividends from the cash flow. Note, by default, dividends are excluded from the cash flow.
Features and procedures for calculating the internal rate of return (IRR) and the modified internal rate of return (MIRR)
☛ Note that only net cash flow (NCF) is used to calculate the IRR internal rate of return and the modified internal rate of return of the MIRR.
In the first case, the rate at which NPV = 0, it is easy enough to choose, using the Excel table. In the example (Excel spreadsheet), the total value of the line "Total Discounted Cash Flow [5] + [6]" is zero if the discount rate is 47.14%.
Example of calculating the internal rate of return - IRR:
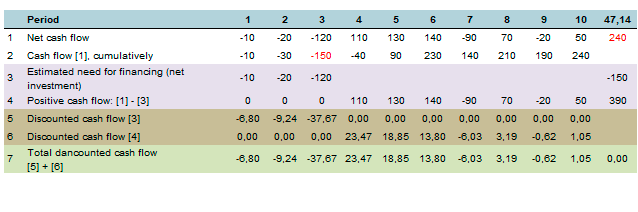
☛ This result is easy to verify using the built-in Excel formula, which is called the IRR (internal rate of return). For this, it is sufficient to enter the value of line [1] "Net cash flow" in the formula in the following format: "= IRR (C2: L2)". The result in either case will coincide.
In the second case, when calculating the MIRR, first one finds the total positive flows (tributaries) and negative flows (outflows). In this example, the discount rate is 11% and the WACC rate is 15%.
Example of calculating the modified internal rate of return - MIRR:
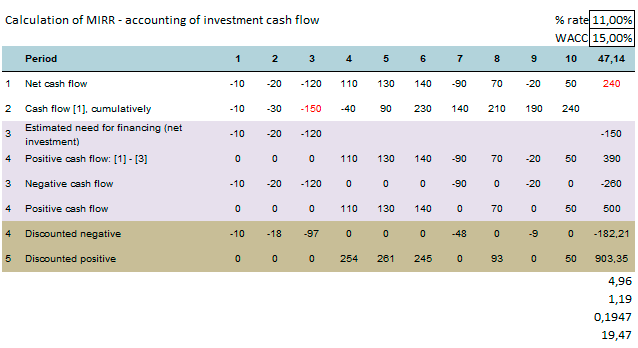
☛ This result is also easily verified using the built-in Excel formula, which is called MIRR (modified internal rate of return). To do this, the line [1] "Net cash flow" is used in the same format: "= MVDD (C2: L2; Discount rate; WACC)". The result in either case will coincide.
Formula MIRR (Modified Internal Rate of Return):
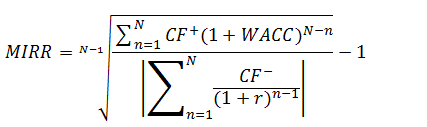
CF+n – incomes of the n-th period (positive values)
CF-n – costs, (investment, reinvestment) of the n-th period
WACC – weighted average cost of capital
r – discount rate
N – duration of the project
To change the settings, see «General settings. Investment analysis».
