Эта статья включена в раздел «Операционное планирование. Модели скользящих средних в BPE» справки "по использованию программы для финансового планирования и анализа Budget-Plan Express для Windows"
Практика применения моделей скользящих средних
Олег Мостовой
(разработчик IT-проектов).
Для модификации ряда, могут быть выбраны любые из 3-х моделей (SMA, WMA и EMA), в зависимости от типа расчетов и данных. Например, при расчете модели WMA в качестве весов может быть выбран номер очередности элемента ряда или показатель смежного ряда (например, объем продаж).
Budget-Plan Express – программный продукт для подготовки бизнес-планов и презентаций в формате Word и Excel.
Cмотрите видеоурок «Пример расчета бизнес-плана с нуля. Проект интернет-магазина – от подготовки данных до отчета бизнес-плана в Word» ...
1. Простое скользящее среднее (SMA) вычисляется по формуле:
-
SMAt = ( Pt + Pt-1 + Pt-2 +… Pt-n+1 ) / n
где
SMAt – значение скользящего среднего в точке t;
n – количество значений ряда, или – сглаживающий интервал.
2. Взвешенное скользящее среднее (WMA) вычисляется по формуле:
-
WMAt = ( Wn*Pt + W(n-1)*Pt-1 + W(n-2)*Pt-2 +… W(n-i+1)*Pt-n+1 ) / [n + (n-1) + (n-2)…(n-n+1)]
где
WMAt – значение скользящего среднего в точке t;
n – количество значений исходного ряда;
Wi – вес взвешенного компонента.
По сути WMA является модификацией модели SMA с добавлением компоненты веса.
3. Экспоненциальное скользящее среднее (EMA) вычисляется по формуле:
-
EMAt = a * Pt + (1 – a) * EMAt-1
где
EMAt – значение скользящего среднего в точке t;
EMAt-1 – значение скользящего среднего в точке t-1;
a – константа сглаживания EMA (smoothing constant), коэффициент изменяющий степень сглаживания, иногда его называют коэффициент определяющий скорость уменьшения весов, он принимает значение от 0 и до 1 (а не равен 0).
При сглаживании рядов и прогнозировании, применяются эти же формулы, с той разницей, что в первом случае расчетный период для SMAt является средним периодом, во втором он – последний, т. е. в случае прогнозирования, расчет основан на предшествующих периодах.
Скользящие средние и краткосрочные прогнозы в рамках адаптивной модели
Экстраполяция тенденции как метод прогнозирования - основа большинства методов прогнозирования, в том числе – в адаптивных моделях на основе скользящих средних – с коротким прогнозным интервалом.
Адаптивные методы позволяют при изучении тенденции учитывать степень влияния предыдущих уровней на последующие значения динамического ряда. К адаптивным методам относятся методы скользящих и экспоненциальных средних, метод гармонических весов, методы авторегрессионных преобразований.
- если необходимо сгладить беспорядочные колебания, то интервал сглаживания берут, как правило, большим (максимальное число уровней - 6);
- если же есть необходимость сохранить периодически повторяющиеся колебания, то интервал сглаживания уменьшают до 3 уровней.
1. Определение интервала сглаживания
Определение интервала сглаживания (числа входящих в него уровней) зависит:2. Алгоритм вычисления при сглаживании
Сглаживание методом скользящей средней заключается в том, что вычисляется средний уровень из 3, 4 и т.д. интервалов. В результате, расчет средней, как бы, скользит от начала ряда динамики к его концу. В моделях SMA и WMA, и их модификациях, степень сглаживания определяется шагом – чем больше шаг, тем выше степень сглаживания. В EMA:– При нечетном шаге каждая вычисленная скользящая средняя соответствует реальному интервалу (моменту) времени, находящемуся в середине шага (интервала), а число сглаженных уровней, меньше первоначального числа уровней на величину шага скользящей средней, уменьшенного на единицу.
– При четном шаге, две средние скользящие центрируются. Операция центрирования заключается в повторном скольжении с шагом, равным двум. Число уровней сглаженного ряда будет меньше на величину шага скользящей средней.
Пример.
Пусть интервал равен 4. Расчет для элемента 3 будет следующим:
| № | Ряд | Формула | Предварительный расчет | Окончательный расчет |
| 1 | 20,00 | |||
| 2 | 21,00 | |||
| 3 | 19,00 | SMAt = (Pt-2+Pt-1+Pt+ Pt+1) / n |
(20+21+19+24)/4=21 | (21+22,5)/2=21,75 |
| 4 | 24,00 | SMAt+1=(Pt-1+Pt+Pt+1+ Pt+2) / n |
(21+19+24+26)/4=22,5 | 26,00 |
| 5 | 20,00 |
Тогда, более удобная формула для реализации алгоритма:
-
SMAt = ½ *(Pt-2+2*(Pt-1+Pt+Pt+1) + Pt+2) / 4
Где:
SMAt – значение простого скользящего среднего в точке t;
n = 4 – сглаживающий интервал.
Когда речь идет о сглаживании ряда, первые и последние значения остаются неизменными, модифицируются значения между первым и последним периодами.
Построение скользящих средних и экстраполяция
В неэкспоненциальных моделях (SMA, WMA) чувствительность сглаживания зависит от выбранного сглаживающего интервала (от 3 - 6).
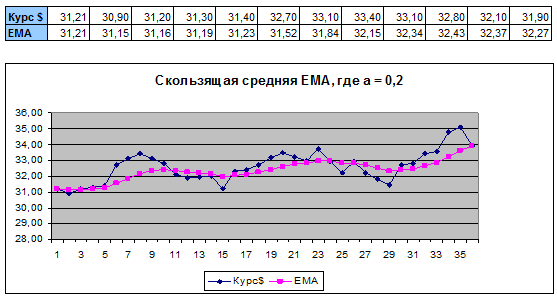
Уровень сглаживания (чувствительность) в экспоненциальной модели (EMA) зависит от константы сглаживания (в примере расчета - от коэффициента a).
Из графика (Пример 1) видно, если выбрать значение константы сглаживания = 1, исходный ряд и расчетный (EMA) - практически совпадут.
При построении скользящих средних и экстраполяции тенденции (краткосрочные прогнозы), используются другие периоды – предшествующие текущему, с установленным интервалом. Здесь при выборе интервала сглаживания нужно понимать две «способности» средних: чувствительность к изменениям и приглушение изменений (от резких колебаний). Соответственно, если вам нужно увеличить чувствительность тренда, интервал должен быть более коротким, и – наоборот. Для EMA чувствительность зависит от коэффициента – a: при a → 1, значения EMAt → к значениям исходного ряда, и – наоборот: при a → 0, значения EMAt → к значениям средней линии ряда.
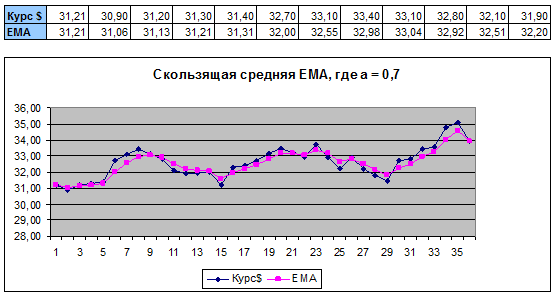
Пример 1.
Сглаживание ряда скользящей средней EMA, с коэффициентом числа а равным 0,7:
Пример 2.
Сглаживание ряда скользящей средней EMA, с коэффициентом числа а равным 0,2:
Выберите лицензию Budget-Plan Express и оплатите в личном кабинете – в рублях или другой валютой
