Факторный анализ
Олег Мостовой
(разработчик IT-проектов).
Назначение факторного анализа
Каждый результирующий показатель зависит от многочисленных факторов. Чем детальней рассматривается влияние факторов на величину показателя, тем точнее результаты анализа и оценка качества принимаемого решения. В некоторых ситуациях, без глубокого и всестороннего изучения прямого влияния факторов нельзя сделать обоснованные выводы о результатах деятельности компании.
Факторный анализ – определение влияния факторов на результат - является одним из сильнейших методических решений в анализе хозяйственной деятельности компаний для принятия решений. Для руководителей - дополнительный аргумент, дополнительный "угол зрения".
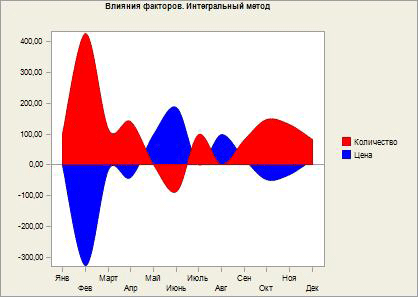
Однако на практике он применяется редко в силу нескольких причин:
1) реализация этого метода требует некоторых усилий и специфического инструмента (программного продукта);
2) у компаний есть другие «вечные» первоочередные задачи.
Еще лучше, если факторный метод анализа (как в нашем случае) «встроен» в финансовую модель, а не является абстрактным приложением.
Budget-Plan Express – программный продукт для подготовки бизнес-планов и презентаций в формате Word и Excel.
Cмотрите видеоурок «Пример расчета бизнес-плана с нуля. Проект интернет-магазина – от подготовки данных до отчета бизнес-плана в Word» ...
Виды факторного анализа
Различают два основных вида факторного анализа – детерминированный и стохастический. Суть стохастического метода – измерение влияния стохастических зависимостей с неопределенными и приблизительными факторами. Стохастический метод целесообразно применять для экономических исследований с неполной (вероятностной) корреляцией: например, для задач маркетинга. Поэтому, говоря о факторном анализе, здесь речь пойдет о детерминированном анализе.
Целесообразность применения факторного анализа
Как известно, анализировать можно все и до бесконечности. Целесообразно на первом этапе реализовать анализ по отклонениям, а там где это необходимо и оправдано - применить факторный метод анализа. Во многих случаях простого анализа по отклонениям достаточно, чтобы понять, что отклонение «критическое», и когда совсем не обязательно знать степень его влияния.
Задачи факторного анализа
История факторного анализа начинается с 1919 года, когда впервые была предложена детерминированная модель Дюпона (The DuPont System of Analysis) для расчета коэффициента рентабельности совокупного капитала (ROA).
Факторный метод анализа часто используется для оценки влияния количества, цены, номенклатуры - на выручку, а также - для анализа структуры маржинальной прибыли, себестоимости, коэффициентных показателей, в методике определения величин резервов, в балансовом методе и для других задач. Для возможности анализа необходимо условие: наличие жесткой связи между факторами. В общем виде она может быть представлена:
-
Υ = ƒ( χ1χ2 …χi), где Υ - результативный признак; χi - факторы влияния
Факторные модели
Различают четыре типа детерминированных моделей:
- Аддитивные модели имеют вид: Υ= Σχi = χ1 + χ2 + …+ χi
- Мультипликативные модели представлены формулой: Υ= Πχi = χ1χ2 …χi
- Кратные модели: Υ = χ1 / χ2
- Смешанные модели: представляют комбинации формул
В детерминированном анализе используются различные методы измерения влияния факторов:
- цепной подстановки;
- абсолютных разниц;
- относительных разниц;
- индексный;
- пропорционального деления;
- интегральный;
- логарифмический.
В первых четырех методах используется прием элиминирования (последовательного исключения влияющих факторов). Более универсальными (с точки зрения использования в моделях) являются интегральный метод и метод цепных подстановок. А самыми точными - интегральный и логарифмический методы.
Практика реализации факторного метода анализа
Также, модели могут быть простыми и каскадными, прямого (от общего к частному) и обратного (изучение причинно-следственных связей) действия, статические и динамические, ретроспективные и прогнозные - в зависимости от целей анализа. Используются приемы преобразования формул: удлинения факторной системы, формального разложения, расширения и сокращения факторных моделей. Для сложных структур на первом этапе описывается модель факторов.
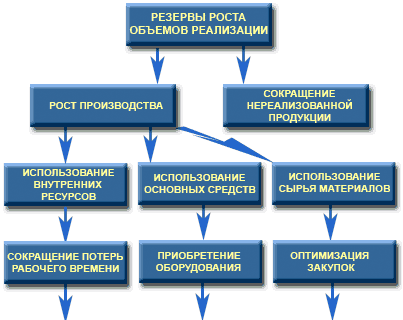
Пример детерминированной структурно-логической модели
Не только с целью установления наличия или отсутствия причинно-следственных связей, направлений связи, но и для того чтобы показать логику влияния факторов: как факторы прямо и косвенно влияют друг на друга.
Многомерное решение
Могут быть построены сегментные модели (что важно для решений управленческого учета), это дает возможность получить факторную модель по различным срезам: ЦФО, регионам, продуктам... в зависимости от того, как сегментирована модель. Графическая визуализация позволяет использовать в полной мере возможности анализа, "проваливаясь" через графики до нижнего уровня данных.
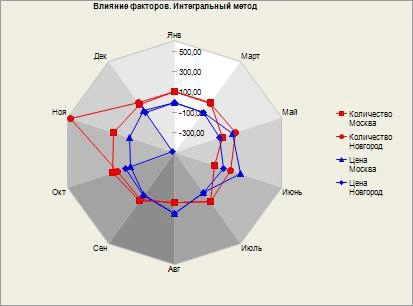
Δ χiу=ƒ(χ1, χ0…χ0)-ƒ(χ1, χ1…χ0)
| Показатель/факторы (%) | янв | фев | март | апр | май | июнь | июль | авг | сен | окт | ноя | дек |
| Отклонение от выручки | -11,3 | -55,28 | 2,49 | -1,27 | 5,7 | 28,12 | 5,0 | 0,0 | 35,9 | 39,76 | 9,95 | 20,55 |
| Отклонение по цене | -1,44 | -0,62 | -2,39 | -7,08 | 0,66 | 9,81 | 0,0 | 0,0 | 8,72 | 4,82 | -2,26 | 4,82 |
| Отклонение по количеству | -10,0 | -55,0 | 5,0 | 6,25 | 5,0 | 16,67 | 5,0 | 0,0 | 25,0 | 33,33 | 12,5 | 15,0 |
| Влияние цены (%) | 11,48 | 0,5 | -100,5 | 591,25 | 12,23 | 40,72 | 0,0 | 100,0 | 30,35 | 16,17 | -25,6 | 27,0 |
| Влияние количества (%) | 88,52 | 99,5 | 200,5 | -491,25 | 87,77 | 59,28 | 100,0 | 0,0 | 69,65 | 83,83 | 125,6 | 73,0 |
Δƒχ = Δχу0 + ½ΔχΔу ; Δƒу = Δуχ0 + ½ΔχΔу
| Влияние цены (%) | 12,12 | 0,81 | -98,1 | 573,86 | 11,94 | 37,82 | 0,0 | 100,0 | 27,32 | 14,15 | -24,18 | 25,24 |
| Влияние количества (%) | 87,88 | 99,19 | 198,1 | -473,86 | 88,06 | 62,18 | 100,0 | 0,0 | 72,68 | 85,85 | 124,18 | 74,76 |
| Погрешность цены (%) | 94,74 | 62,07 | 102,44 | 103,03 | 102,44 | 107,69 | 102,44 | 100,0 | 111,11 | 114,29 | 105,88 | 106,98 |
| Порешность количества (%) | 100,73 | 100,31 | 101,21 | 103,67 | 99,67 | 95,32 | 100,0 | 0,0 | 95,82 | 97,65 | 101,15 | 97,65 |
Основные методы. Достоинства и недостатки
Элиминирование имеет ряд существенных недостатков:
- Порядок показателей в расчетах должен быть строго определен: нужно следить за тем, чтобы на первом месте стояли количественные, затем - качественные показатели, а также – за численным порядком показателя. Иначе результат будет неверно рассчитан.
- Недостаточная точность расчетов.
- В многофакторных моделях или с маленькими значениями влияющих факторов может не дать результатов (это видно уже на этапе элиминирования).
В некоторых случаях, применение элиминирования не дает решения.
Выводы. Интегральный и логарифмический методы лишены недостатков методов с использованием элиминирования и являются наиболее точными, но используются не во всех моделях: нельзя использовать в аддитивных моделях, а логарифмический метод можно использовать только в мультипликативных моделях. Поэтому, видимо, предпочтительнее использовать интегральный или логарифмический методы, а в аддитивных моделях – любой из методов с использованием элиминирования.
